MOFET의 기본 structure 및 동작원리에 대해서 살펴보았다.
이번엔 MOSFET의 I/V 특성(전류-전압 특성)에 대해서 공부해보려고 한다.
반도체 물리를 기반한 어려운 수식이 대거 나올 예정인데 최대한 직관적으로 이해할 수 있도록 서술했다.
모바일 환경에서는 TeX 수식 변환이 안되므로 데스크탑 환경에서 보는 것을 권장한다.
2022.02.17. 초안
2022.02.17.수정1
2.2 MOS I/V Characteristics
우리는 2.1 MOS Device에서 어떻게 channel이 형성되고 전류가 흐를 수 있는 지에 대해서 알아보았다.
이번 chapter에서는 각 terminal의 전압에 따라서 얼마만큼의 전류가 흐르는지 I/V Characteristics에 대해서 살펴볼 예정이다.
2.2.1 Threshold Voltage
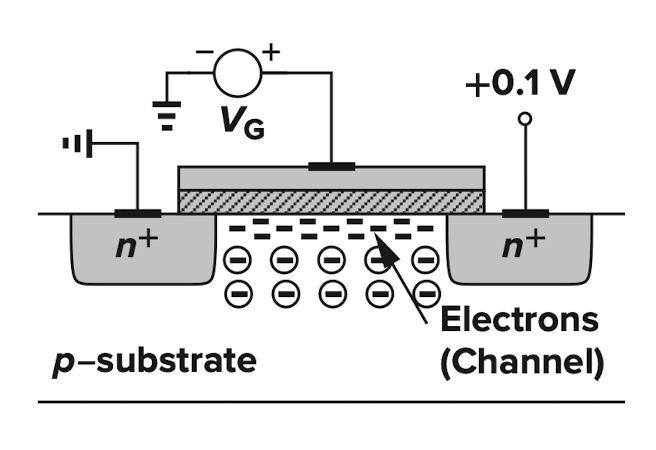
NMOS에서 Gate 전압을 계속 키우다보면, Oxide 아래(interface)에 electron이 모여서 channel을 이루게 되고 이 channel을 통해서 Source와 Drain 사이에 전류가 흐를 수 있게 된다. 그래서 이 channel을 형성하는데 필요한 Gate 전압을 Threshold voltage(문턱 전압)이라고 한다.
더 엄밀한 정의는, Oxide interface의 carrier(NMOS에서는 electron) concentration이 substrate의 doping(NMOS에서는 p) concentration과 동일해지는 Gate 전압이다. Oxide interface와 substrate를 비교하면 마치 doping concentration은 같고 doping-type만 반대인 것처럼 볼 수 있어서 이를 보고 inversion이라고 한다.
threshold voltage, $V_{th}$의 수식은 아래와 같다.
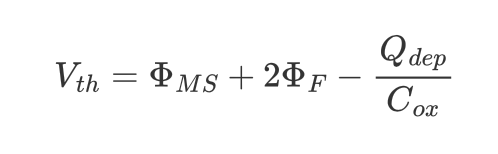
간단히 각 term들을 설명하면(자세한 설명은 appendix 참조)
- $\Phi_{MS}$는 Gate metal과 Silicon substrate의 work function(or Fermi-level)의 차이이다.
- $\Phi_F$는 substrate의 intrinsic Fermi-level과 (extrinsic) Fermi-level의 차이이다.
- $-\tfrac{Q_{dep}}{C_{ox}}$는 Gate 전압이 분배되어서 Oxide dielectrics에 걸리는 전압이다.
2.2.2 I/V Characteristics
Triode Region
이제 I/V 특성에 대해 살펴보자.
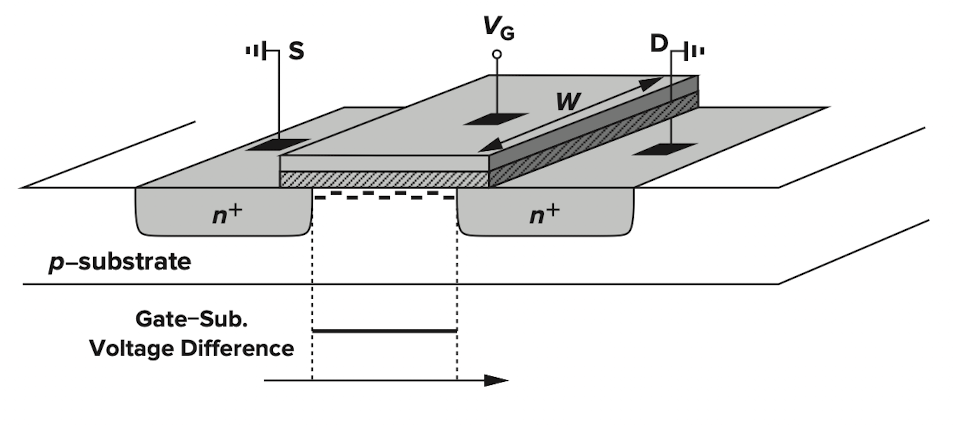
$V_G>V_{th}$이면 Oxide interface에 channel이 형성된다. 이때 inversion된 channel의 총 전하량 $Q$과 는 다음과 같다.
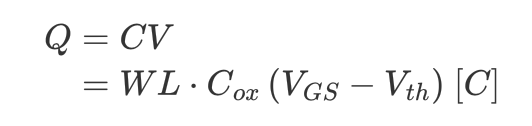
$C_{ox}$는 Oxide의 단위 면적당 capacitance이므로 width, $W$와 length, $L$을 곱해야 전체 전하량이 된다. Sorce-Drain 방향을 x-axis로 뒀을 때 normalize한 전하량 $Q_{inv}$는 다음과 같다.
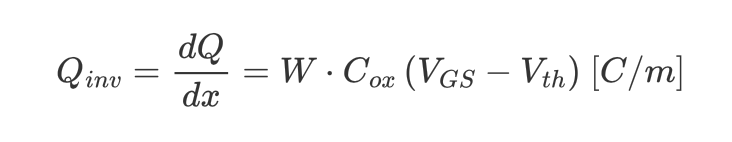
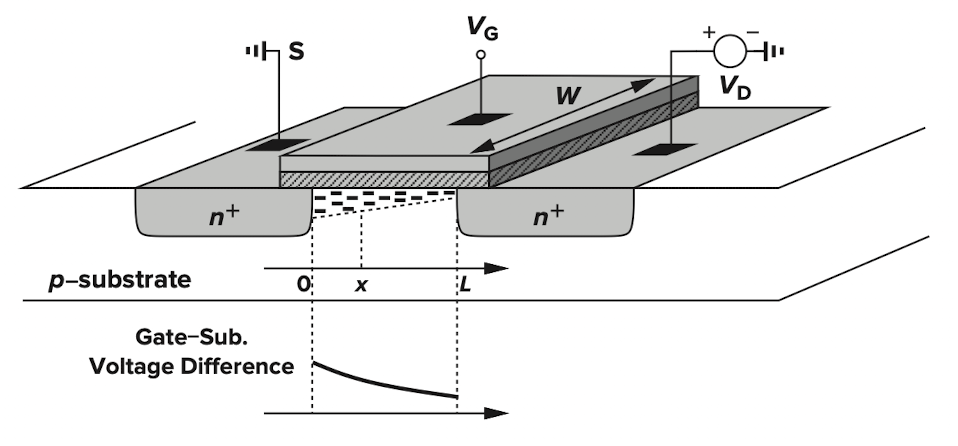
이 상태에서 Drain 전압을 걸면 증가시키면 channel에 lateral 방향의 자기장이 형성되고 위치에 따라서 인가된 전압이 다르다. 즉, 전하량이 달라진다.
위치에 따른 전하량 $Q_{inv}\left(x\right)$는 다음과 같다.
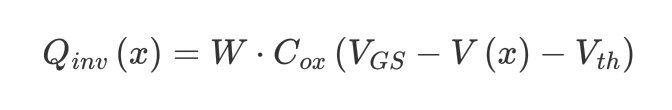
이제 Drain과 Source 사이의 전류를 구해보자.
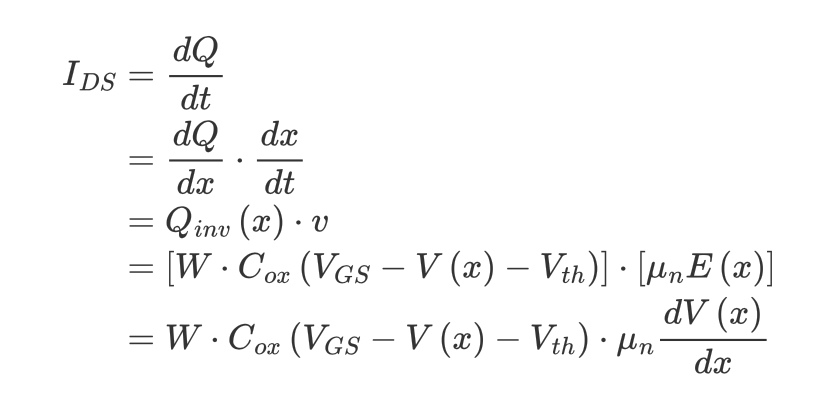
$v$는 carrier의 velocity고 $E(x)$는 channel의 lateral 방향의 eletric field의 크기이다.
우리는 위치에 따른 channel의 전압 $V(x)$에 대한 전류식을 유도하였는데, 위치에 따른 channel 전압과 그것의 미분값을 매번 구할 수 없다. 그래서 boundary condition $V(x=0)=V_S$와 $V(x=L)=V_D$, 직렬이므로 모든 $x$에 대해서 $I_{DS}$가 동일한 점을이용해서 1st-order differential equation을 풀어낸다.
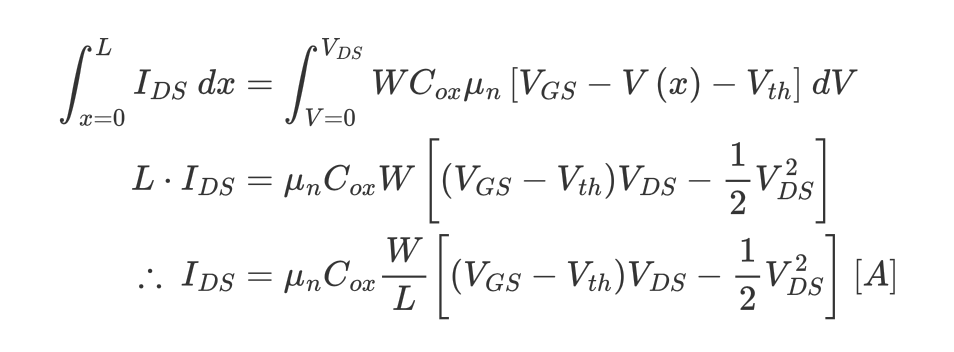
$V_{GS}-V_{th}$는 Gate 전압이 MOSFET을 turn-on시키기 위한 전압($V_{th}$)를 제외하고 추가적으로 인가된 Gate 전압이 얼마인지 나타낸다. 그래서 이 값을 overdrive voltage(과구동 전압), $V_{ov}$로 정의한다.
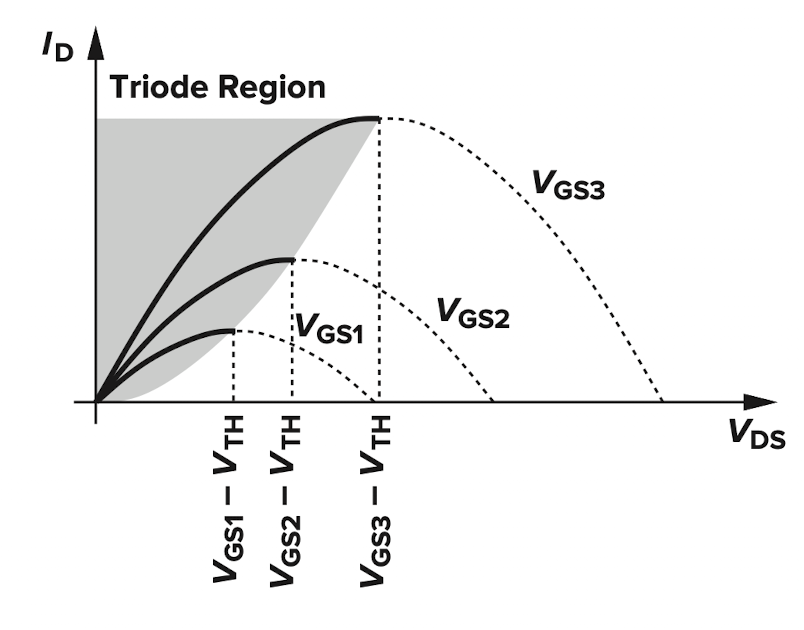
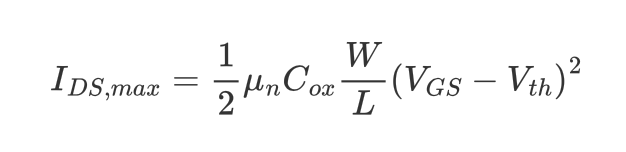
$V_{DS}$에 대한 $I_{DS}$의 curve는 위와 같다. 우리가 구한 $I_{DS}$의 수식 대로면, $V_{DS}=V_{GS}-V_{th}$에서 maximum current를 만들어낸다.(2차함수이므로 완전제곱형으로 고쳐보면 쉽게 알 수 있다.) 그리고 $V_{GS}>V_{th}$이고 $V_{DS}<V_{GS}-V_{th}$인 case를 Tridoe Region(or Linear Region)이라고 한다.
Saturation Region
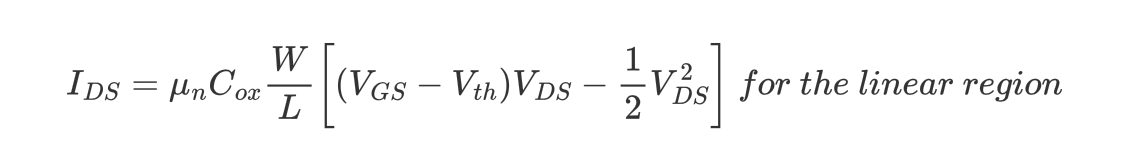
$I_{DS}$ 수식에서, $V_{DS}>V_{GS}-V_{th}$이면 어떻게 될까. 수식대로라면 $I_{DS}$는 $V_{DS}=V_{GS}-V_{th}$에서 maximal value를 가진 뒤 감소한다. 하지만 실제로 Drain current가 감소하지는 않는다.
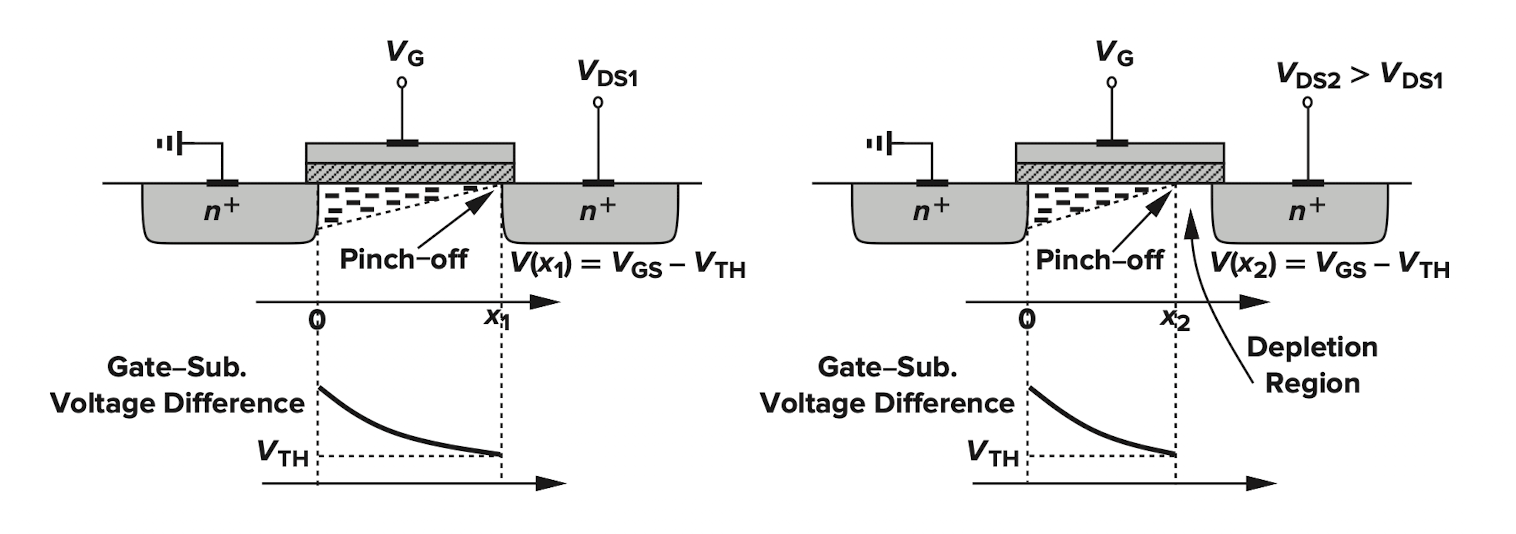
$V_{DS}=V_{GS}-V_{th}$이면 Drain에 맞닿는 부근의 channel의 전하량이 0이 되고 이를 Pinch-off라고 한다.(Drain 전압이 증가하면 Drain 부근의 substrate의 potential이 증가하므로 inversion이 되기 위한 전압이 부족해진다) 그 상태에서 $V_{DS}$를 더 증가시키면, Pinch-off되는 지점이 점점 Source 방향으로 이동하게 된다. Pinch-off 부근과 Drain 사이에는 depletion region이 형성된다. 이 depletion region에 의해, Source에서 Pinch-off point로 온 charge가 Drain으로 보내지면서 전류를 흐르게 한다.
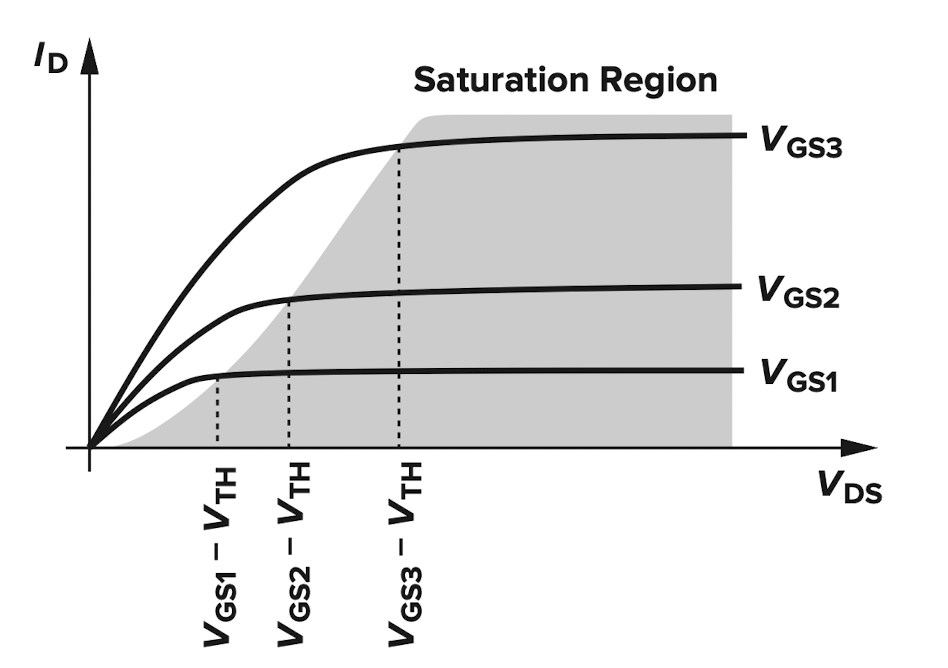
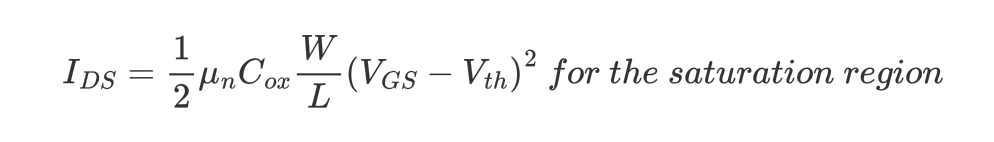
결과적으로 $V_{DS}>V_{GS}-V_{th}$인 경우, Pinch-off가 되어 $V_{DS}$가 증가하더라고 전류가 더이상 증가하지 않고 그대로 유지된다. 그래서 $V_{GS}>V_{th}$이고 $V_{DS}>V_{GS}-V_{th}$인 case를 Saturation Region이라고 한다.
Drain current는, triode region과 saturation region에서 Drain-Source voltage의 2차 함수로 표현되는데, 이러한 전류-전압 관계식을 보고 Square-law라고 한다.
To sum-up
각 terminal voltage에 따를 Drain current는 다음과 같다.
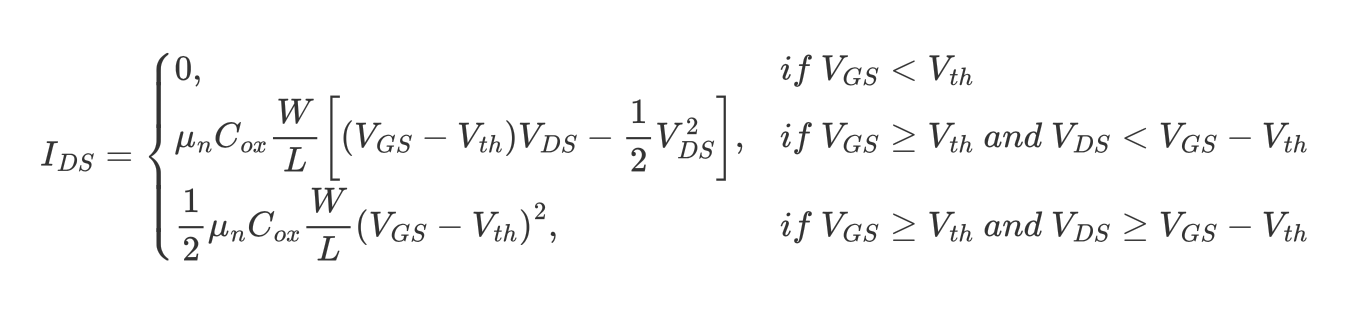
순서대로 각각 Cut-off region, Triode region(or Linear region), Saturation region이다.
2.2.3 Transconductance
MOSFET은 Gate에 걸리는 전압을 Drain 전류로 변환해주는 역할을 한다고 볼 수 있다. 그래서 MOSFET의 전압-전류 변환에 대한 Figure-Of-Merit(FOM)을 transconductance라고 정의한다.
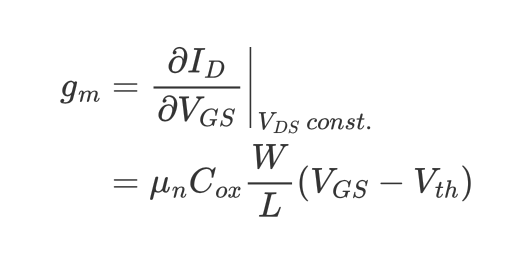
transconductance, $g_m$은 MOSFET이 주어진 $V_{DS}$에서 $V_{GS}$를 $I_{DS}$로 얼만큼 변환할 수 있는지에 대한 평가지표(Figure-Of-Merit)이다. $I_{DS}$의 수식으로 부터 $g_m$을 아래와 같이 유도할 수도 있다.
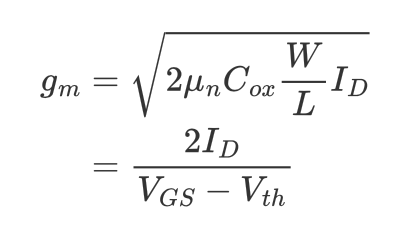
Appendix
Threshold Voltage
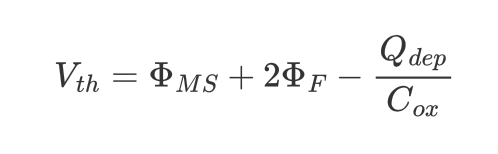
threshold voltage에 대해 조금 더 자세히 살펴보자.(Energy-band model, Fermi level, Electron affinity 등을 모르겠으면 그냥 넘어가자)
- $\Phi_{MS}$
$\Phi_{MS}$는 Gate metal과 Silicon substrate의 work function(or Fermi-level)의 차이이다.
Metal-Oxide-Semiconductor 구조에서 Gate metal에 poly-Si를 사용했다고 가정하자. Gate와 substrate의 electron affinity는 동일(둘다 $Si$이므로)하지만 doping type, doping concentration의 차이(Gate의 poly-Si는 metal처럼 동작해야해서 low-resistivity를 위해 heavily doping을 함)로 Fermi-level에 차이가 생긴다. 그래서 equilibrium state에서도 Oxide interface 부근의 Energy-band에 bending이 존재한다. 이러한 bending을 없애고 substrate의 Energy-band를 flat하게 만들어주기 위한 전압이라고 생각하면 된다. - $2\Phi_{F}$
$\Phi_F$는 substrate의 intrinsic Fermi-level과 (extrinsic) Fermi-level의 차이이다.
intrinsic semiconductor(un-doped)에 doping을 하면 (extrinsic) Fermi-level이 변한다. 그래서 Oxide interface에 intrinsic과 extrinsic Fermi-level의 차이($\Phi_F$)만큼의 potential(정확히는 $\Phi_{surface}=\Phi_{MS}+\Phi_F$)이 걸리면, intrinsic Fermi-level과 extrinsic Fermi-level이 동일해져서 interface에서는 carrier concentration이 마치 intrinsic semiconductor과 같아진다. 여기에 $\Phi_F$만큼의 potential을 더 걸어주면($\Phi_{surface}=\Phi_{MS}+2\Phi_F$) interface의 carrier concentration이 substrate의 doping concentration과 동일하면서 doping type은 반대인 것과 동일한 inversion상태가 된다. - $-\dfrac{Q_{dep}}{C_{ox}}$
Gate 전압에서 Oxide dielectrics에 걸리는 전압이다.
depletion region도 Capcitor의 일종($\tfrac{dQ}{dV}\neq 0$)이므로 Gate 전압은 Oxide와 depletion region에 분배되서 인가된다. (앞의 $\Phi_{MS}+2\Phi_F$가 depletion region에 인가되어서 Oxide interface에 걸리는 potential이다) Capacitor에서 전압은 $Q=CV$에서 유도할 수 있다. 이때, $Q$는 Capacitor에서 $V$의 + 방향에 charge이고 우리가 살펴볼 substrate의 charge $Q_{sub}$는 $V$의 -방향의 charge 이므로 $Q=-Q_{sub}$이다. $Q_{sub}$는 inversion된 charge, $Q_{inv}$과 depletion region의 charge, $Q_{dep}$의 합인데, inversion이 된 직후 상태에서는 $Q_{inv}\ll Q_{dep}$이라서 $Q_{sub}=Q_{inv}+Q_{dep} \approx Q_{dep}$으로 근사된다. 따라서 Oxide에 걸리는 전압 $V_{ox}$는 $\tfrac{Q}{C}\approx-\tfrac{Q_{dep}}{C_{ox}}$이다.
'전자공학 > Circuits' 카테고리의 다른 글
| [MOSFET 03] Second-order Effect (0) | 2022.02.17 |
|---|---|
| [MOSFET 01] Basic MOS device (0) | 2022.02.14 |
| Introduction of Analog Design (0) | 2022.02.14 |


